بنگاه دانش اقتصاد *ابتهاج*
مقالات آموزشی اقتصادی صهیب عبیدیبنگاه دانش اقتصاد *ابتهاج*
مقالات آموزشی اقتصادی صهیب عبیدیدرباره من
درود بر شما!
امیدوارم مطالب این تارنما مورد پسند شما قرار بگیرد و ما را با نظرات نیکتان همت افزایی کنید.
سپاس از شما
ابتهاج عبیدی
ebtihaj.ib@gmail.com
ادامه...
روزانهها
همه- دانشنامه فارسی اقتصاد بزرگترین دانشنامه فارسی اقتصاد
- ۱۰۰۰ عدد کارت ویزیت رایگان متخصص در طراحی و چاپ کارت ویزیت و امور تبلیغات ، 1000 عدد کارت ویزیت رایگان ، جک و اس ام اس
- ریاضیات زیباست A weblog about math and mathematics in persian language
- بیائید گام به گام کمپیوتر بیاموزیم وبلاگ اختصاصی کمپیوتر رازمحمد نورزی پکتیاوال
- حق و صبر بهترین سایت درباره تاریخ و فرهنگ مردم ممتاز شرق میانه
- فرهنگ فارسی به فارسی فرهنگ دهخدا
- بهمن۹۳ شخصی آموزشی معلوماتی جالب
- قلم (رسم الخط) های فارسی و انگلیسی بهترین مرجع قلم های فارسی و انگلیسی
- از هر دهن سخنی همه چیز از هر جا.. هر چیز را در این سایت ببینید... کتاب.فلم.آموزش.دانستنی.نرم افزار.عشق.عکس
- حسابدار اولین وبلاگ فارسی زبان با موضوعیت حسابداری که از سال ۱۳۸۰ فعالیت خود را آغاز کرده است
- اقتصاد و اصلاحات منتخبی است از مجموع مقالات و مصاحبه های دانشمندان اقتصاد
- دیکشنری تصویری آنلاین مریام-وبستر دیکشنری تصویری آنلاین مریام-وبستر. انگلیسی به انگلیسی
- لنک وبلاگ بنگاه دانشجویان افغانی لنک وبلاگ بنگاه دانشجویان افغانی در گوگل پیج
- چند روز از عمرتان می گذرد تاریخ تولدتان را وارد کنید تا بدانید چند روز از عمرتان می گذرد
- سایت آموزش سیاست و روابط بین المللی سایت آموزشیی سیاست و روابط بین المللی.مطیع الله مطیع
- خانه ریاضیات اصفهان همه چیز در مورد ریاضی
- محاسبه سن شما در سیارات دیگر تاریخ تولد خود را به میلادی بنویسید تا سن خود را در سیارات دیگر مشاهده کنید
- رسم نمودار بصورت آنلاین نمودارهای دو بعدی و سه بعدی را رسم کنید .
- حل انتگرال بصورت آنلاین جواب انتگرال نامعین را بصورت آنلاین مشاهده کنید .
- ضریب هوشی خود را مشخص کنید . آی کیو تیست
- محاسبه میانگین ؛میانه ؛ مد و دامنه تغییرات بصورت آنلاین میانگین ؛میانه ؛ مد و دامنه تغییرات ..Mean, Median and Mode
- محاسبات هندسی بصورت آنلاین در این سایت می توانید محاسبات هندسی مانند مساحت و محیط و ... را آنلاین انجام دهید.
- فکر می کنید چقدر عمر می کنید ؟ این سایت انگلیسی است و از شما اطلاعاتی را گرفته و عمر شما را پیش بینی می کند ، بااینکه این سایت علمی است ولی والله اعلم .
- حرفهای جامعه امروزی از هر دهن سخنی
- گروه اقتصادی گروه اقتصادی خبر گذاری فارس
- The Hall of Afghan Economists - English
- بنگاه اقتصادی دانشجویان افغان
- جست وجوی پیشرفته جست وجوی پیشرفته در گوگل
- Greg Mankiw's Blog -وبلاگ گریگوری منکیو Random Observations for Students of Economics
- ان الدین عندالله الاسلام عناوین٬ مقالات٬ کتب و سمعیات پیرامون دین مبین اسلام (صهیب عبیدی ابتهاج)
- دکشنری آنلاین فرهنگ فارسی به انگلیسی و انگلیسی به فارسی آنلاین
- گوگل فارسی گوگل به زبان خودمان...پارسی
- مقالات مدیریتی مقالات مدیریتی
- مدیران ایران پایگاه جامع اطلاع رسانی مدیران ایران
- کتابخانه مرکزی ایران
- میگ ایران هر نوع مقالات
- رستک دریچه ای به اندیشه اقتصاد آزاد
- ابتهاج در سایت متخصصین
- همیم سایت علمی همیم جان به لسان پشتو
- تقویم شمسی تقویم شمسی- هر ماه در پی دی اف
- البوم پولهای افغانی آلبوم عکس پول (بانک نوت) های افغانی
- نقشه اینترنت نقشه استعمال انترنت در سرتاسر جهان
- رسامی جالب چهره دوستت (دختر یا پسر) را رسم کن.
- برگه انترنتی آموزشی عبدالله مسعود شما میتوانید موضوعات اقتصادی را درینجا بخوانید
- New Economist
- Ebtihaj in Javanblog Javan Blog
- مقالات آموزشی مکرومیدیا هر نوع مقاله وغیره
پیوندها
- تاپ ۱۰۰ وبلاگ اقتصادی
- اسلایدهای کتاب مبانی اقتصاد کلان مدرن
- وبلاگ آموزشی اقتصادی قدوسی
- New Economist
- سایت بوسه....مقالات جالب اقتصادی
- سایت تفریحی ابتهاج
- سایت علمی ابتهاج
- بورس نیویارک-New York Stock Exchange
- بورس توکیو - Tokyo Stock Exchange
- فدراسیون جهانی بورس ها - World Federation of Exchanges
- وزارت اقتصاد افغانستان
- وزارت صنعت و تجارت افغانستان
- وزارت مخابرات افغانستان
- وزارت امور اقتصادی و دارایی ایران
- وزارت مالیه افغانستان
- بانک انکشاف آسیایی - افغانستان
- وزارت صنایع و معادن ایران
- بانک جهانی - افغانستان
- نگاهی به اقتصاد (بحث گروهی)
- راهکارهای اقتصادی
- نگاهی عمیق به اقتصاد
- لبخند ریاضی
- سایت ریاضی حسین دنبلی
- انستیتیوت مطالعاتی افغانستان
- تبادل اسعار
- فورم انکشافی افغانستان
- CIA Fact Book on Afghanistan - Economy
- Afghanistan Investment and Reconstruction Task Force
- afghan chamber of commerce
- محاسب زکات
- دانش مدیریت
- پروژه به زبان ساده
- کتاب های ((اقتصاد کلی)) گریگوری منکیو-N. Gregory Mankiw
- تجارت اینترنتی
- مبانی مدیریت اسلامی
- لینکستان اقتصاد و توسعه
- لینک های اقتصادی
- گزیده های مدیریت (مجلات)
- نشریات مدیریتی
- برو بچه های ریاضی
- ریاضی دروازه علوم است
- دانشگاههای سراسر جهان
- بانک اطلاعات نشریات سراسر کشور در همه رشته ها
- آژانس آلکا گشت
- افغان کامپیوتر
- روزگاران
- سفارت کبرای افغانستان در انقره ترکیه
- بهمن۹۳
- شبکه قلب آسیا
- حق و صبر
- بانک مقلات علمی وتخصصی
- پښتو کمپیوټر پوهنه
- کانون وبلاگنویسان افغانستان
- لغت نامه تخصصی حسابداری
- ریاضیات زیباست
- بنی فضل
- اولین پایگاه اینترنتی مهندسان و دانشجویان صنایع دانشگاه آزاد واحد
- بزرگترین دانشنامه اقتصاد بزبان فارسی
دستهها
- ابتدائیه و سلام 30
- داونلود کتاب ها و مجلات اقتصادی 150
- موضوعات اقتصادی - Economics 374
- موضوعات ریاضیاتی - Mathematics 80
- مدیریت و اداره - Management 240
- بازاریابی - Marketing 64
- روابط تجاری - Bus. Communication 28
- نرم افزار های اقتصادی و ریاضیاتی 36
- بانکداری - Banking 37
- مقالات محوری و ساحوی 159
- افغانستان عزیز 42
- بورس - Stock Exchange 18
- دانشمندان شهیر اقتصاد و مدیریت 24
- اخبار اقتصادی افغانستان 44
- آموزش.... 25
- تجارت - Business 39
- اقتصاد اسلامی 35
- موضوعات انگلیسی - English Topics 4
- ای میل این ویب سایت و گروپ گوگل 8
- روان شناسی - Psychology 29
- بیمه - Insurance 9
- اخبار اقتصادی 26
- پول (Money) 13
- نظریه بازی ها - Game Theory 4
- مالیات - Taxes 6
- شرکت ها سهامی-Corporations 5
- بانکداری اسلامی-Islamic Banking 17
- به هر کودک یک لپ تاپ 1
- بازار جهانی ارز - For Ex 4
- بازار جهانی موتر ها-W.V.Mkt 4
- تستهای هوش (ریاضیاتی) 3
- ارز 3
- صنعت - Industies 1
- تجارت الکترونیکی - E-Business 3
- پول الکترونیک - E-Money 1
- مجموعه مقالات 27
- توسعه اقتصادی 1
- پولشویی - Money Laundry 4
- اقتصاد جهان-World Economy 14
- سرمایه - Capital 2
- بازار های جهانی 3
- فایل های پاورپوینت قابل داونلود 6
- ربا (سود) - Interest 6
- ایزو یا مدیریت کیفیت - ISO 10
- مدیریت اسلامی 2
- نظرات شما عزیزان 3
- بحران مالی کنونی جهان 26
- سایت اکونوپیدیا - Econopedia 39
برگهها
جدیدترین یادداشتها
همه- دانشنامه اقتصاد و مدیریت
- واژه های برتر دانشنامه اقتصاد
- ابرواژه های دانشنامه اقتصاد و مدیریت
- آغاز چهارمین سال فعالیت دانش نامه اقتصاد و مدیریت
- تبلیـغات تصویـری فرهنـگی در متـروی پاریـس
- تازه های دانشنامه اقتصاد و مدیریت
- لغتنامه ها در اینترنت
- چینی ها برای جذب گردشگر چه کارها که نمی کنند ...
- مارکهای تقلبی را بهتر بشناسیم ...
- بـررسی ارزش جهانـی پـول ایـران از 300 سال پیـش تا به امـروز
- تصـایری از تبلیـغات مبتـکرانه و مفـهومی!
- بهتـرین راهـکارهای کاربـردی برای مـطالـعه
- انتشار پنج گزارش جهانی در آغاز سال ۲۰۱۲
- نوروز و سال جدید خورشیدی 1391 مبارک
- اصول و آداب مدیریت...
- بهترین راهکارهای کاربردی برای مطالعه
- رونمایی از اسکناس های پلاستیکی، پایان مبارزه کانادا با پول کاغذی
- شناخت بهتر فساد مالی سه هزارمیلیارد تومانی !
- دانشنامه دوساله شد
- تازه ترین مطالب بزرگترین دانشنامه اقتصاد و مدیریت
- تازه ترین مطالب دانشنامه اقتصاد و مدیریت
- دانشنامه فارسی اقتصاد - ۶ نومبر ۲۰۱۰
- فهرست دانشنامه فارسی اقتصاد
- دانشنامه فارسی اقتصاد با یک ملیون بازدید در ماه جهانی شد
- برچسپ های پربازدید دانشنامه
- کشف معادن تازه در افغانستان...
- فهرست مطالب دانشنامه
- مطالب تازه وارده در تارنمای دانشنامه
- لطفا اینجا نظر دهید...
- دانشنامه اقتصاد
- بهترین سرویس برای کسب اعتبار رایگان کاربران
- تا می توانید انرژی مثبت بگیرید
- حکایت موفقیت - ۲
- حکایت موفقیت - ۱
- تازه های دانشنامه - صفحه اصلی
- تازه های دانشنامه
- دانشنامه در چند ماه اخیر
- مطالب تازه
- اقتصاد از دانشنامه اقتصاد
- دانشنامه در نول گوگل
- دانشنامه بعد از چهار ماه
- دانشنامه ۱۷ دسامبر سال ۲۰۰۹
- بروز شدن دانشنامه فارسی اقتصاد
- دانشنامه فارسی اقتصاد - دوشنبه ۱۶ نومبر
- ۱۲ مطلب تازه سایت دانشنامه
- ۱۰ مطلب پربازدید این هفته
- دانشنامه بعد از گذشت دوماه
- مطالب پربازدید و مطالب تازه سایت دانشنامه
- دانشنامه - سه شنبه ۱۳ اکتبر ۲۰۰۹
- دانشنامه فارسی اقتصاد
نویسندگان
- ابتهاج عبیدی 1717
بایگانی
- اردیبهشت 1392 1
- مرداد 1391 3
- تیر 1391 2
- اردیبهشت 1391 5
- فروردین 1391 3
- آذر 1390 2
- آبان 1390 2
- شهریور 1390 1
- خرداد 1390 1
- فروردین 1390 1
- آبان 1389 1
- مهر 1389 2
- تیر 1389 1
- خرداد 1389 3
- اردیبهشت 1389 6
- فروردین 1389 2
- اسفند 1388 2
- بهمن 1388 1
- دی 1388 2
- آذر 1388 2
- آبان 1388 4
- مهر 1388 4
- شهریور 1388 2
- مرداد 1388 3
- تیر 1388 2
- خرداد 1388 15
- اردیبهشت 1388 17
- فروردین 1388 9
- اسفند 1387 2
- بهمن 1387 17
- دی 1387 34
- آذر 1387 21
- آبان 1387 115
- مهر 1387 17
- شهریور 1387 5
- تیر 1387 2
- خرداد 1387 10
- اردیبهشت 1387 64
- فروردین 1387 73
- اسفند 1386 169
- بهمن 1386 120
- دی 1386 68
- آذر 1386 160
- آبان 1386 411
- مهر 1386 330
آمار : 688877 بازدید
Powered by Blogsky
قضیه لاگرانژ
اگر یک گروه متناهی و
یک گروه متناهی و  باشد و
باشد و  که
که  آنگاه
آنگاه 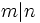 .
.
اثبات:
می دانیم تعداد اعضای همدسته
چپ زیرگروه 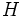 ، با یکدیگر برابر است. یعنی :
، با یکدیگر برابر است. یعنی :

همچنین میدانیم گروه
 توسط همدستههای دو به دو متمایز
توسط همدستههای دو به دو متمایز 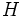 ، افراز میشود ، لذا:
، افراز میشود ، لذا:
با توجه به اینکه  ؛ پس تعداد متناهی همدسته چپ
؛ پس تعداد متناهی همدسته چپ  ، مثلاً
، مثلاً  تا وجود دارند که :
تا وجود دارند که : 
بطوریکه اشتراک  ها
ها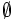 است
است
بنابراین:
شاخص.
عدد که در قضیه لاگرانژ مطرح شد، تعداد همدسته های چپ متمایز
که در قضیه لاگرانژ مطرح شد، تعداد همدسته های چپ متمایز 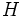 در
در  را معرفی مینماید .
را معرفی مینماید .  را اندیس (شاخص یا نشان )
را اندیس (شاخص یا نشان ) 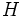 در
در  مینامند و آن را با نماد
مینامند و آن را با نماد 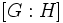 نمایش میدهند.
نمایش میدهند. لازم به ذکر است که این تعریف برای همدستههای راست متمایز نیز درست است.
نتیجه.
- اگر
 و
و  گروه متناهی باشد ، آنگاه
گروه متناهی باشد ، آنگاه 
- مرتبه هر عضو گروه متناهی
 ، مانند
، مانند  ،
مرتبه
،
مرتبه  را عاد میکند. یعنی
را عاد میکند. یعنی 
- هر گاه
 گروه متناهی باشد ، بطوریکه
گروه متناهی باشد ، بطوریکه  و
و عددی اول باشد ، آنگاه
عددی اول باشد ، آنگاه  یک گروه دوری است و زیرگروه محض نابدیهی ندارد. (تنها زیرگروه محض آن ، تولید شده توسط عنصر خنثی ، یعنی
یک گروه دوری است و زیرگروه محض نابدیهی ندارد. (تنها زیرگروه محض آن ، تولید شده توسط عنصر خنثی ، یعنی
 است)
است)
نکته.
عکس قضیه لاگرانژ همواره درست نیست.
ابتهاج عبیدی
1387/08/06 ساعت 11:42 ق.ظ
برای نمایش آواتار خود در این وبلاگ در سایت Gravatar.com ثبت نام کنید. (راهنما)




















































ایمیل شما بعد از ثبت نمایش داده نخواهد شد